我们在小学里就接触过素数,也叫质数,这玩意儿概念我就不讲了,大家都知道哈。直到目前为止,素数仍然是一个常常被提及和使用的东西。我们在电脑和网络的加密算法中,最常用一种叫做 RSA 非对称加密算法,其对可靠性的仰仗就是目前为止我们并没有很好的数学工具解决极大整数的因数分解问题,因此如果该算法中提供的整数是由 2 个极大素数相乘获得,那就是 RSA 可靠性的保障了。至今为止,人们还在研究,不断地在寻找着一些尽可能大的素数,最新成果是在 2018 年 12 月 7 日,专家通过互联网梅森素数大搜索(GIMPS)项目宣布发现了已知最大的素数:\(2^{82,589,933}-1\),共有 24,862,048 位。
当然,本文在下面所述的方法并不适合让科学家们去寻找极大素数,不然要那 GIMPS 干啥去?我们这里旨在对小素数进行寻找罗列,而列出所有小素数最有效的方法之一,就是埃拉托斯特尼筛法(sieve of Eratosthenes)了,这是一种简单且历史悠久的筛法,从古希腊时期便已发现并开始使用了。
埃氏算法的核心思想就是:给出要筛数值的范围 n,找出 \(\sqrt {n}\) 以内的素数 \(p_{1}, p_{2}...,p_{k}\)。先用 2 去筛,即把 2 留下,把 2 的倍数剔除掉;再用下一个素数,也就是 3 筛,把 3 留下,把 3 的倍数剔除掉;接下去用下一个素数 5 筛,把 5 留下,把 5 的倍数剔除掉;不断重复下去……
举个简单的例子,下面是找出 16 以内的素数步骤:
1. 列出 2-16 之间自然数的所有序列:
2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16
2. 标出序列中的第一个质数,也就是 2,并将 2 的倍数划去:
2, 3,
4, 5,6, 7,8, 9,10, 11,12, 13,14, 15,16\(\rightarrow\) 2, 3, 5, 7, 9, 11, 13, 15
3. 之前序列中最大数的平方根为 \(\sqrt {16}\), 大于 2, 继续筛选,将 3 标出,在剩余的数中划去 3 的倍数:
2, 3, 5, 7,
9, 11, 13,15\(\rightarrow\) 2, 3, 5, 7, 11, 13,
4. 再来判断,\(3 < \sqrt {16}\) 继续筛选,标出下一个数 5,划去剩余数列里 5 的倍数(也没的划了)
\(\rightarrow\) 2, 3, 5, 7, 11, 13
5. 此时 5 已经大于等于 \(\sqrt {16}\) 了,不用再继续筛选了,剩下的数字都是素数了!
2, 3, 5, 7, 11, 13
给张 GIF 图体会一下:
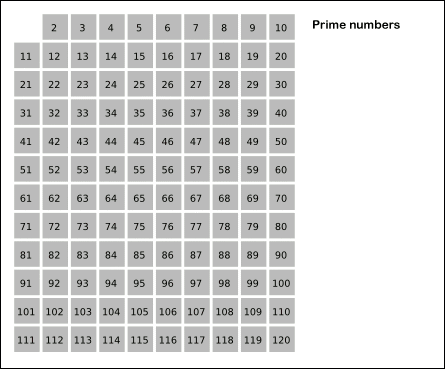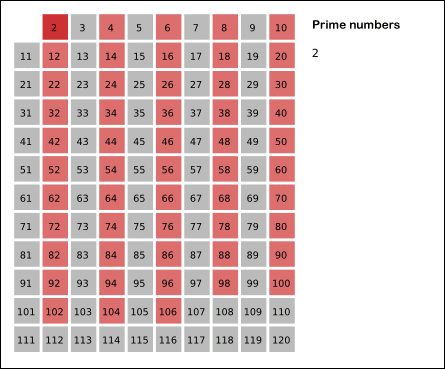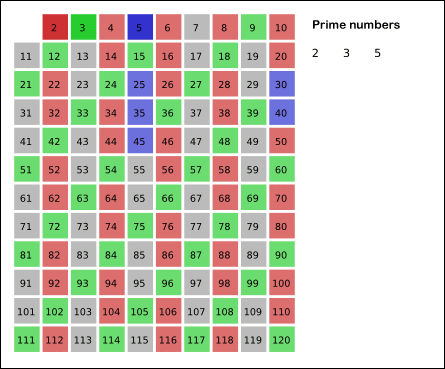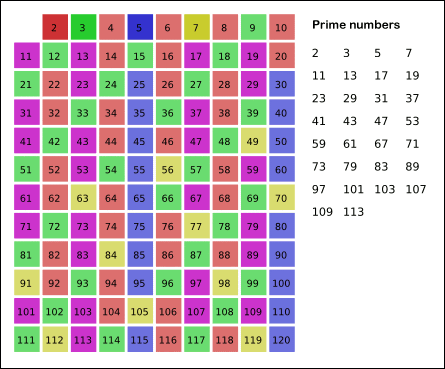
这个筛选法使得我们无需历遍检查数列中的每一个数,只需历遍到最大值的 \(\sqrt {n}\) 为止即可,这种针对小素数的筛查方法可真算得上效率极高。
在 wiki 上,人家给出了一些程序语言的算法 demo,例如 Python:
def eratosthenes(n):
IsPrime = [True] * (n + 1)
IsPrime[1] = False #1不为素数
for i in range(2, int(n ** 0.5) + 1):
if IsPrime[i]:
for j in range(i * i, n + 1, i):
IsPrime[j] = False
return {x for x in range(2, n + 1) if IsPrime[x]}
if __name__ == "__main__":
print(eratosthenes(120))
今天我们的主要目的,就是要用 JS 来实现一遍,搞懂了埃氏筛法的原理后,我们接下来可以开始动手了!首先我们要构建一个数组,以整数 n 为界,内容为 [2, 3, 4,...n],然后对这个数组进行唐氏埃氏筛查。
// 方法一:传统循环法生成 [2, 3, 4,...100]
let n = 1, numArr = []
while(n++ < 100) numArr.push(n)
恩不错,把代码放到 console 里执行以下,没问题,但有没有其他的生成方式呢,当然有!我们用 ES2015 之后数组新增加的原生方法 Array.from 再来实现一下:
// 方法二:利用 Array.from 实现
const numArr = Array.from({ length: 100 }, (v, i) => i+1).slice(1)
嗯,一行代码搞定啦!代码虽然简洁了,但是效率如何呢?把 limit 放到两千万,在最新版本的 Google Chrome(v73)测试执行时间,结果发现,姜还是老的辣,还是传统的循环方式更为高效。接下来继续在最新版本的 Firefox(v66) 和 Safari (v12.1) 上跑执行时间,虽然各个浏览器内核可能对 Array.from 进行了一定的实现优化,但依旧是方法一领先,快了大概 2-4 倍以上,好吧,方法一胜!
(在这里需要提醒一下,如果将以上测试代码放到 codepen 的沙盒中执行测试,反而是方法二的执行时间领先,真是见鬼啊,不用管它,我们只认在纯浏览器环境中的测试结果。)
有了之前的准备,我们可以写个很简单的方法,生成一个自然数序列,再通过 isPrime 方法过滤这个数组,最后我们就能得到该范围内的素数集合了:
// 返回参数范围内的所有质数,默认边界 100
function getPrime (limit = 1e2) {
let n = 1, numArr = []
while(n++ < limit) numArr.push(n)
return numArr.filter(isPrime)
}
function isPrime (v) {
let i = 2, len = Math.sqrt(v)
for (; i <= len; i++) {
if (v % i === 0) return false
}
return true
}
console.log(getPrime(20)) // [2, 3, 5, 7, 11, 13, 17, 19]
嗯,貌似很简单,真的这么简单?还能更简单吗?不造啊!但是,我在网上却见到一个判断素数的奇技淫巧,我们可以看这段代码:
let a = 199, b = 198
!/^,?$|^(,,+?)\1+$/.test(Array(++a)) // true
!/^,?$|^(,,+?)\1+$/.test(Array(++b)) // false
我也是醉了,这个正则 /^,?$|^(,,+?)\1+$/ 魔力这么巨大吗?不过奉劝各位,这个东西还是不要用的好,效率奇差,我写了个测试用来判断 10000 以内的素数时,浏览器已经假死了,这段代码咱还是藏起来供上的好,哈哈!
后记
为了这个奇葩正则,我后来上网查到一篇文章:《检查素数的正则表达式》,大致弄明白了其中的原理,从这个正则的处理方式来看,效率的确是比较低的。要使用这个正规则表达式,你需要把自然数转成多个 1 的字符串,如:2 要写成 “11”, 3 要写成 “111”, 17 要写成“11111111111111111”。
仔细看这篇文章所给出的正则:/^1?$|^(11+?)\1+$/,它把我之前的“,”换成了“1”,经过我的测试,一万以内的素数历遍,执行时间从 7 秒多一下减小到 500 多毫秒,不过这和用纯粹的埃氏算法相比,仍然相差了两个数量级。孰优孰劣,高下立判,不过这还是无法掩盖用正则来判断素数这种风骚的走位方式,效率低点就地点吧,就当回手掏一把了。
